1 前言

或许你也跟我一样，打完 CSP2025 后学习了这个知识点 —— AC 自动机。

首先如果您没有学过 KMP 和 Trie 字典树，建议还是先看一下，这里只要求掌握 KMP 的思想即可，不用太熟练。

因为我在最开始学习 AC 自动机的时候对 KMP 的理解也不是很深，所以对于这个算法也是有所畏惧的，但是稍微深入一点，你会发现他实际上没有你想象的那么难，个人感觉甚至还没有 KMP 难吧。

最后，如果想学好 AC 自动机，就请先放下 KMP，理解好 Trie，专心阅读。这样或许对你更有帮助！

KMP：前缀函数与 KMP 算法 - OI Wiki

Trie：字典树（Trie） - OI Wiki

2 基础的 AC 自动机

模式串：待匹配入文本串的字符串
文本串：被匹配的字符串
AC 自动机应用：给出若干个模式串和一个文本串，求每个模式串在文本串中出现的次数，或者是是否出现。—— 多模式匹配

2.1 概述

一个 AC 自动机由两个部分组成：

• 基础的 Trie 树：将所有模式串全部加入一棵 Trie 树
• KMP 的思想：对 Trie 树上的所有节点构造 Fail（失配）指针。

我们将利用它进行多模式匹配。

2.2 Trie 的构建

Trie 构建这部分的代码很简单，每次给出一个单词添加到 Trie 里面就可以了。

static const int SIGMA=; // 最多有多少个分支 
static const int MAXN=; // 所有模式串的总长度之和（最多分支节点） + 1（根节点）

struct Node {
    int nxt[SIGMA]; // 该节点的子节点，没有是 0
    int fail; // 后面会讲到

    Node() {
        memset(nxt,0,sizeof(nxt));
        fail=0;
    }
};

vector<Node> tr; 

void init() {
    tr.reserve(MAXN);
    tr.push_back(Node()); // root = 0
}

static int id(char c) { // 用于返回处理后的 id （把边权从其他类型转到编号）
    return c-'A'; // 这是个例子，将 'A'~'Z' 转换到编号 0~25，方便 nxt 存储 
}

void insert(string s) { // 添加一个模式串到 Trie
    int u=0;
    for (char c:s) {
        int v=id(c);
        if (!tr[u].nxt[v]) {
            tr[u].nxt[v]=tr.size();
            tr.push_back(Node());
        }
        u=tr[u].nxt[v];
    }
}

// 建议使用 struct 或者 class，方便开多个

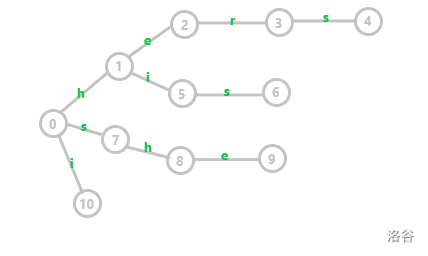
假设现在我们有模式串 i、he、his、she、hers，那我们构建的 Trie 树如下：

假设现在我们有文本串 𝚜𝚑𝚎𝚛𝚜𝚑𝚎𝚒𝚜𝚑𝚒𝚜。

我们能用文本串在 Trie 上进行匹配，会先经过 $7、8、9$ 三个点，然后就无法匹配了，这时候难道我们要回到根节点重新开始吗？

不，这样效率太慢了。这时候我们想到了 KMP，它运用了 nxt 指针加速，我们也可以引用同样的方案，在找不到可匹配内容的时候跳到另一个地方。

2.3 失配指针（Fail）的构建

我们先来回顾一下失配指针的作用。如果当前文本串 T 已经匹配到了某一个点 i，则下一位 T_{i+1} 应该匹配到 Trie 树当前节点下边权为 T_{i+1} 相连的节点。我们称当找不到该相连节点时应该跳到的点就是当前点的失配指针。

我们该如何求出这个指针呢？假设当前我们找到的区间是 [l, r]，则当我们在 Trie 中找到一个可以与文本串匹配的儿子并且下跳时，是增加 r 的动作。所以失配指针应该是增加 l 的动作（因为肯定是从左往右匹配啊）。这是我们很容易发现，对于相同的 r，变化前的 l_1 与变化后的 l_2 （l_1 < l_2，因为要增加 l）肯定保证 [T_{l_2},T_r] 是 [T_{l_1},T_r] 的后缀。如果此时 r 向右移动一位，那么我们还是满足 [T_{l_2},T_r] 是 [T_{l_1},T_r] 的后缀，所以如果一个点的父节点的失配指针有一个边权为当前点到父节点边权的点，那么这个点就应该是当前节点的失配指针。

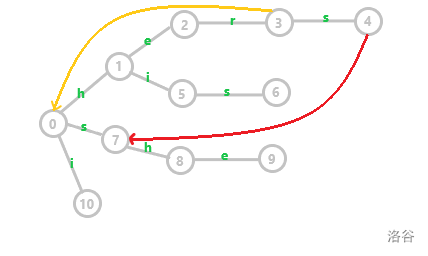
这个可能有点难理解，我们来看一张图。

黄色边是我们已知的失配指针，3 号节点的子节点 4 号节点，失配指针便是 0 号节点下方对应边权同样为 s 的 7 号节点。（4 号节点的失配指针为红色边）

那如果黄色边指向的节点没有对应的同样边权的节点呢？那我们就应该找父节点失配指针的失配指针，直到根节点或者有对应边权的子节点为止。因为失配指针找的是后缀，又有 b 是 a 的后缀，且 c 是 b 的后缀即可推断出 c 是 a 的后缀，我们可以说：（根节点到）当前节点的失配指针 f（的路径）是（根节点到）当前节点（的路径）的后缀，且（根节点到）f 的失配指针（的路径）是（根节点到）f（的路径）的后缀。

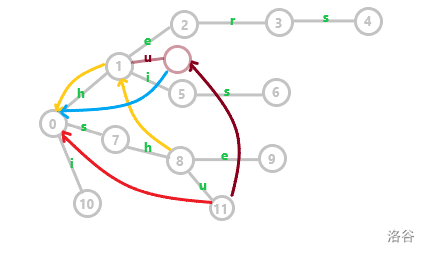
这里同样给出一张图为例：

淡红是虚点，因为找不到，所以沿着蓝色边（1 的失配指针，黄色边）跳到根节点，红色边是 11 号节点的失配指针。

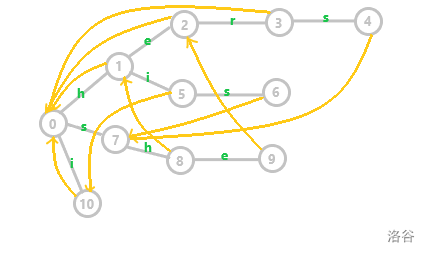
最后，我们只需要初始化所有根节点的子节点的失配指针指向根节点即可，根节点自环（下图未标明）。这里给出除根节点外的所有失配指针示意。

我们应该如何用代码实现失配指针的构建呢？很好证明的一点是，失配指针指向的节点深度一定小于当前节点深度。因为（根节点到）当前节点的失配指针（的路径）是（根节点到）当前节点（的路径）的后缀，后缀长度小于原串长度，自然深度也较小。所以如果我们按照深度一层一层遍历构造失配指针，是不会发生找不到父节点失配指针的情况的，于是我们可以使用 BFS。

void build() {
    queue<int> q;

    for (int c=0;c<SIGMA;c++) {
        int v=tr[0].nxt[c];
        if (v) {
            tr[v].fail=0; // 初始化
            q.push(v);
        } else {
            tr[0].nxt[c]=0; 
        }
    }

    while (!q.empty()) {
        int u=q.front();
        q.pop();
        for (int c=0;c<SIGMA;c++) {
            int v=tr[u].nxt[c];
            if (v) {
                tr[v].fail=tr[tr[u].fail].nxt[c]; // 只更新失配指针
                q.push(v);
            } else {
                tr[u].nxt[c]=tr[tr[u].fail].nxt[c]; // 失败的时候自动跳转到失配指针
            }
        }
    }
}

到这里，一个基础的 AC 自动机模板就已经完成了，我们先把它封装一下。

struct ACor {
    static const int SIGMA=::SIGMA; 
    static const int MAXN=::MAXN; // 所有模式串的总长度之和 + 1（根节点）
    
    struct Node {
        int nxt[SIGMA]; 
        int fail;

        Node() {
            memset(nxt,0,sizeof(nxt));
            fail=0;
        }
    };

    vector<Node> tr; 

    ACor() {
        tr.reserve(MAXN);
        tr.push_back(Node()); // root=0
    }

    static int id(int c) { 
        return c; 
    }

    void insert(string s) {
        int u=0;
        for (char c:s) {
            int v=id(c);
            if (!tr[u].nxt[v]) {
                tr[u].nxt[v]=tr.size();
                tr.push_back(Node());
            }
            u=tr[u].nxt[v];
        }
    }

    void build() {
        queue<int> q;

        for (int c=0;c<SIGMA;c++) {
            int v=tr[0].nxt[c];
            if (v) {
                tr[v].fail=0;
                q.push(v);
            } else {
                tr[0].nxt[c]=0;
            }
        }

        while (!q.empty()) {
            int u=q.front();
            q.pop();
            for (int c=0;c<SIGMA;c++) {
                int v=tr[u].nxt[c];
                if (v) {
                    tr[v].fail=tr[tr[u].fail].nxt[c];
                    q.push(v);
                } else {
                    tr[u].nxt[c]=tr[tr[u].fail].nxt[c];
                }
            }
        }
    }
};

3 查询模式串出现次数

3.1 算法流程

刚刚我们构建完了 Fail 指针，现在我们要把它用起来。还是那个例子，𝚜𝚑𝚎𝚛𝚜𝚑𝚎𝚒𝚜𝚑𝚒𝚜。（模式串：i、he、his、she、hers）

[TODO ACor-Fail.png]

文本串的第 $1$ 位是 s，我们到达 $7$ 号节点；

文本串的第 $2$ 位是 h，我们到达 $8$ 号节点；

文本串的第 $3$ 位是 e，我们到达 $9$ 号节点，找到单词 she；

文本串的第 $4$ 位是 r，这时候 $9$ 号节点下没有边的边权为 r，我们直接走 Fail 指针（缩左端点）到达 $2$ 号节点，找到单词 he；

文本串的第 $5$ 位是 s，这时候 $2$ 号节点下没有边的边权为 s，我们直接走 Fail 指针（缩左端点）到达根节点；

文本串的第 $6$ 位是 h，我们到达 $1$ 号节点；

文本串的第 $7$ 位是 e，我们到达 $2$ 号节点，找到单词 he。此时，你或许会发现，到了这一位还可以匹配一个单词 she，但是我们没有统计到，这是因为左端点被 Fail 指针缩的太短了，没有统计到左端点更小的结果。这时候我们开始反思，因为如果有一个单词同样满足在这一位结束且没被统计到，一定是因为这个单词的长度大于当前找到的单词的长度，所以当前单词一定是它的后缀，这也就是失配指针的定义。所以每次找到一个失配指针，失配指针指向节点 Fail[u] 要记录起始节点 u 统计的答案。回到这里，我们要把 $9$ 统计到的答案放到 $2$ 中，成功找到单词 she；

文本串的第 $8$ 位是 i，这时候 $2$ 号节点下没有边的边权为 i，我们直接走 Fail 指针（缩左端点）到达根节点；

文本串的第 $9$ 位是 s，我们到达 $7$ 号节点；

文本串的第 $10 位是 h，我们到达 $8 号节点；

文本串的第 $11 位是 i，这时候 $8 号节点下没有边的边权为 i，我们直接走 Fail 指针（缩左端点）到达 $2$ 节点，$2$ 节点有边的边权为 i，跳到 $5$ 节点；

文本串的第 $12 位是 s，我们到达 $6 号节点，找到单词 his。

到这里，我们就成功模拟完一整个过程了，总结一下，构建的时候对于每个节点 u，Fail[u] 都要记录 u 的答案（包括从其他节点用失配指针转换到 u 的答案，以此类推），防止出现左端点不够长的问题。现在我们知道了流程，来做一做例题。

例题一：P3808 AC 自动机（简单版）

题目描述：给定 n 个模式串 s_i 和一个文本串 t，求有多少个不同的模式串在文本串里出现过。

这时候我们需要在每个节点添加一个参数 vector<int> out，存储当前节点可以匹配到的模式串 ID。

struct Node {
    int nxt[SIGMA]; 
    int fail;
    vector<int> out;

    Node() {
        memset(nxt,0,sizeof(nxt));
        fail=0;
        out.clear();
    }
};

在每次 insert 操作时，最后到达的节点的 out 应该添加该节点的编号，因为只要到达这个点，文本串里一定会有一个当前模式串。

void insert(string s,int id) {
    int u=0;
    for (char c:s) {
        int v=id(c);
        if (!tr[u].nxt[v]) {
            tr[u].nxt[v]=tr.size();
            tr.push_back(Node());
        }
        u=tr[u].nxt[v];
    }
    tr[u].out.push_back(id);
}

当然，我们的 build 函数也需要修改。比如文本串是 she，只考虑其中的两个模式串 he 和 she，这时候我们的自动机会找到图中的 9 号节点，但是并不会找到 2 号节点，这时候会漏记。所以在每次得到一个 fail 指针后，fail 指针节点的 out 应该传递给当前节点。

void build() {
    queue<int> q;

    for (int c=0;c<SIGMA;c++) {
        int v=tr[0].nxt[c];
        if (v) {
            tr[v].fail=0;
            q.push(v);
        } else {
            tr[0].nxt[c]=0;
        }
    }

    while (!q.empty()) {
        int u=q.front();
        q.pop();
        for (int c=0;c<SIGMA;c++) {
            int v=tr[u].nxt[c];
            if (v) {
                tr[v].fail=tr[tr[u].fail].nxt[c];
                tr[v].out.insert(tr[v].out.end(),tr[tr[v].fail].out.begin(),tr[tr[v].fail].out.end());
                q.push(v);
            } else {
                tr[u].nxt[c]=tr[tr[u].fail].nxt[c]; 
            }
        }
    }
}

这时候我们就可以做最后一步啦，统计是否出现。直接根据文本串的字符在 AC 自动机上走一步即可。

int query(string t) {
    int u=0;
    int ans=0;
    map<int,bool> mp; // 之前是否统计过，可以换成数组
    for (char c:t) {
        int v=id(c);
        u=tr[u].nxt[v];  // 自动根据 fail 跳转
        for (auto i:tr[u].out) { // 统计答案
            if (!mp.count(i)) { mp[i]=true,ans++; }
        }
    }
    return ans;
}

例题二：P3796 AC 自动机（简单版 II）

这道题和上一道差距不大，只需要稍微修改一下查询函数即可。

int query(string t) {
    int u=0;
    map<int,int> mp; // 统计出现次数
    for (char c:t) {
        int v=id(c);
        u=tr[u].nxt[v];  // 自动根据 fail 跳转
        for (auto i:tr[u].out) { // 统计答案
            mp[i]++;
        }
    }
    int ans=-1; mp[ans]=LLONG_MIN;
    for (auto it:mp) {
        if (it.second>mp[ans]) ans=it.first;
    }
    return ans;
}

3.2 拓扑排序优化

咱们先来看一道题，P5357 【模板】AC 自动机。

看完题目，你会发现好像跟上一道题一模一样？可以提交了代码，却是 TLE。

考虑优化。

我们先看一个性质，把所有点的失配指针重新构成一个图，它一定是一个 DAG。证明：每个节点的失配指针一定指向深度更低的点（前面说过），就一定不会有环。

因为每个节点的贡献不仅包括它自己，还有深层节点向它的贡献，我们可以先求出当前节点的贡献（它被访问了几次），再通过刚刚用失配指针构成的 DAG 向前转移，就可以得到每个节点的真实贡献了。以这个节点结束的模式串在文本串中出现的次数也就是这个节点的真实贡献。

又因为我们需要无后效性才能更好的传递，不然一个点被一条指针更新一次，传递到下一个节点，这个点又被另一个指针更新，又要再次传递，这样效率就非常低下。于是我们想到可以让每个点都先被更新完（所有指针的已经对其赋值），再传递到下一个，这实际上就是一个拓扑排序的过程。

总结一下，我们先在 Trie 上根据文本串跑一遍，记录每个经过点的贡献为 $1$，然后找到在仅由 Fail 指针构成的图中入度为 $0$ 的点入队，跑一遍拓扑排序，对于每个 u 都将其答案传递给它的失配指针即可。

例题三：P5357 【模板】AC 自动机

这道题便是要用到上面的拓扑排序优化，我们总共分 $4$ 个步骤优化我们的代码。

因为我们要记录每个节点的真实贡献，所以我们要在结构体中新加一个变量 mcnt；
因为我们要记录每个节点的入度，所以我们要在结构体中新加一个变量 rd：

struct Node {
    int nxt[SIGMA]; 
    int fail;
    vector<int> out;
    int mcnt;
    int rd;

    Node() {
        memset(nxt,0,sizeof(nxt));
        out.clear();
        fail=0;
        mcnt=0;
        rd=0;
    }
};

每个经过的点都要让真实贡献 mcnt 加一。

void assign(const string& s) {
    int u=0;
    for (auto c:s) {
        int v=id(c);
        u=tr[u].nxt[v];
        tr[u].mcnt++;
    }
}

我们还需要修改 build 函数，预处理入度。

void build() {
    queue<int> q;

    for (int c=0;c<SIGMA;c++) {
        int v=tr[0].nxt[c];
        if (v) {
            tr[v].fail=0;
            q.push(v);
        } else {
            tr[0].nxt[c]=0;
        }
    }

    while (!q.empty()) {
        int u=q.front();
        q.pop();
        for (int c=0;c<SIGMA;c++) {
            int v=tr[u].nxt[c];
            if (v) {
                tr[v].fail=tr[tr[u].fail].nxt[c];
                tr[tr[v].fail].rd++; // v -> tr[v].fail
                q.push(v);
            } else {
                tr[u].nxt[c]=tr[tr[u].fail].nxt[c]; 
            }
        }
    }
}

最后，我们需要添加一个 topu 函数，把他们两个封装起来。

vector<int> topu(int m/**out 中最大的数字**/) {
    queue<int> q;
    for (int i=0;i<tr.size();i++) {
        if (!tr[i].rd) q.push(i);
    }
    vector<int> ans(m+1,0);
    while (!q.empty()) {
        int u=q.front(); q.pop();
        for (auto i:tr[u].out) {
            ans[i]=tr[u].mcnt;
        }
        int v=tr[u].fail;
        tr[v].mcnt+=tr[u].mcnt;
        if (!--tr[v].rd) q.push(v);
    }
    return ans;
}

vector<int> match(string p,int m) {
    assign(p); return topu(m);
}

这道题就可以通过了。

3.3 完整模板

到这里，我们已经彻底掌握 AC 自动机查询模式串出现次数的题型了，我们把这个题型的最终模板放一下：

struct ACor {
    static const int SIGMA=::SIGMA; 
    static const int MAXN=::MAXN; // 所有模式串的总长度之和+1（根节点）
    
    struct Node {
        int nxt[SIGMA]; 
        int fail;
        vector<int> out;
        int mcnt;
        int rd;

        Node() {
            memset(nxt,0,sizeof(nxt));
            out.clear();
            fail=0;
            mcnt=0;
            rd=0;
        }
    };

    vector<Node> tr; 

    ACor() {
        tr.reserve(MAXN);
        tr.push_back(Node()); // root=0
    }

    static int id(char c) { // 用于返回nxt_id
        return -----; // TODO 转义  
    }

    void insert(string s,int _id) {
        int u=0;
        for (char c:s) {
            int v=id(c);
            // cerr << v << " " << tr[u].nxt[v] << endl;
            if (!tr[u].nxt[v]) {
                tr[u].nxt[v]=tr.size();
                tr.push_back(Node());
            }
            u=tr[u].nxt[v];
        }
        // cerr << _id << " " << u << endl;
        tr[u].out.push_back(_id);
    }
    void assign(const string& s) {
        int u=0;
        for (auto c:s) {
            int v=id(c);
            u=tr[u].nxt[v];
            tr[u].mcnt++;
        }
    }
    void build() {
        queue<int> q;

        for (int c=0;c<SIGMA;c++) {
            int v=tr[0].nxt[c];
            if (v) {
                tr[v].fail=0;
                q.push(v);
            } else {
                tr[0].nxt[c]=0;
            }
        }

        while (!q.empty()) {
            int u=q.front();
            q.pop();
            for (int c=0;c<SIGMA;c++) {
                int v=tr[u].nxt[c];
                if (v) {
                    tr[v].fail=tr[tr[u].fail].nxt[c];
                    tr[tr[v].fail].rd++; // v -> tr[v].fail
                    q.push(v);
                } else {
                    tr[u].nxt[c]=tr[tr[u].fail].nxt[c]; 
                }
            }
        }
    }
    vector<int> topu(int m/**out 中最大的数字**/) {
        queue<int> q;
        for (int i=0;i<tr.size();i++) {
            if (!tr[i].rd) q.push(i);
        }
        vector<int> ans(m+1,0);
        while (!q.empty()) {
            int u=q.front(); q.pop();
            for (auto i:tr[u].out) {
                ans[i]=tr[u].mcnt;
            }
            int v=tr[u].fail;
            tr[v].mcnt+=tr[u].mcnt;
            if (!--tr[v].rd) q.push(v);
        }
        return ans;
    }

    vector<int> match(string p,int m) {
        assign(p); return topu(m);
    }
};